New Article: Planar Models of Street Networks

My article, “Planarity and Street Network Representation in Urban Form Analysis,” was recently published in Environment and Planning B: Urban Analytics and City Science. Models of street networks underlie research in urban travel behavior, accessibility, design patterns, and morphology. These models are commonly defined as planar, meaning they can be represented in two dimensions without any underpasses or overpasses. However, real-world urban street networks exist in three-dimensional space and frequently feature grade separation such as bridges and tunnels: planar simplifications can be useful but they also impact the results of real-world street network analysis. This study measures the nonplanarity of drivable and walkable street networks in the centers of 50 cities worldwide, then examines the variation of nonplanarity across a single city. While some street networks are approximately planar, I empirically quantify how planar models can inconsistently but drastically misrepresent intersection density, street lengths, routing, and connectivity.

A planar graph can be drawn on a two-dimensional plane without any of its edges crossing each other, except where they intersect at nodes. If it cannot be drawn to meet this criterion, it is nonplanar. Street networks are embedded in space, which provides them with geometry (such as geographical coordinates, lengths, areas, shapes, and angles) along with their topology. This creates a minor wrinkle when we consider planarity: we must distinguish between a graph’s mathematical/topological planarity, which we refer to as “formal planarity,” and the planarity of its real-world spatial embedding, which we refer to as “spatial planarity.”

For example, a street network might be spatially nonplanar due to its embedding in space (i.e., it contains overpasses or underpasses in the real world), but it could still be formally planar. That is, if we “re-draw” the graph by moving its nodes and edges around in space without changing how they connect to one another (i.e., altering its geometry without altering its topology), there may exist some alternative spatial embedding that prevents edges crossing anywhere but at nodes. In such a case, the street network is formally planar from a topological perspective, but its real-world embedding is spatially nonplanar.

In the urban studies literature, street networks are commonly modeled as planar graphs. Many street networks are obviously nonplanar in reality, but researchers use planar models as a potentially useful simplification of real-world complexity. However, modeling urban street networks as planar graphs can bias urban form analyses in several ways. 1, intersection counts are overestimated due to false nodes where grade-separated edges cross. 2, average edge lengths are underestimated. 3, connectivity is misrepresented for routing, accessibility analysis, and topological studies.

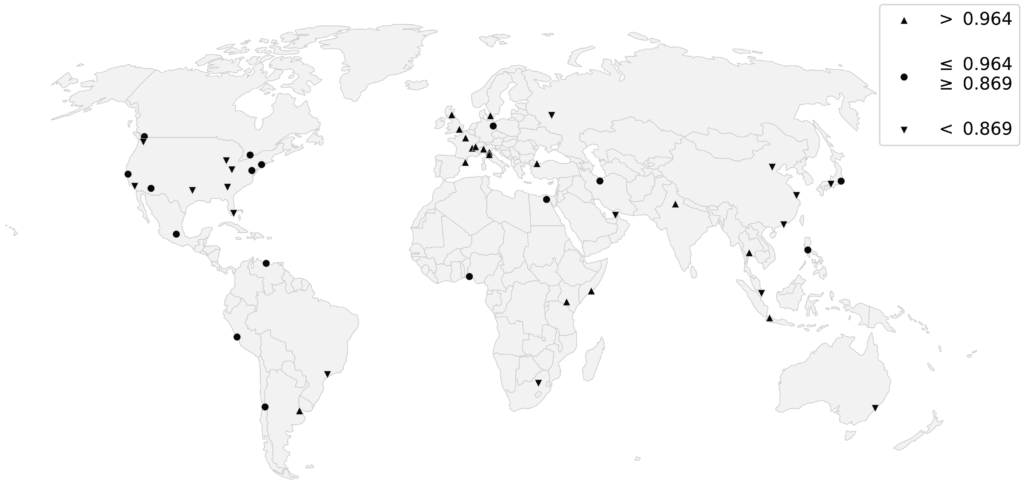
This study develops two new indicators – the Spatial Planarity Ratio and the Edge Length Ratio – then measures the extent of nonplanarity in street networks around the world using OSMnx. For more, read the article.