R-tree Spatial Indexing with Python

Check out the journal article about OSMnx, which implements this technique.

A spatial index such as R-tree can drastically speed up GIS operations like intersections and joins. Spatial indices are key features of spatial databases like PostGIS, but they’re also available for DIY coding in Python. I’ll introduce how R-trees work and how to use them in Python and its geopandas library. All of my code is in this notebook in this urban data science GitHub repo.

An R-tree represents individual objects and their bounding boxes (the “R” is for “Rectangle”) as the lowest level of the spatial index. It then aggregates nearby objects and represents them with their aggregate bounding box in the next higher level of the index. At yet higher levels, the R-tree aggregates bounding boxes and represents them by their bounding box, iteratively, until everything is nested into one top-level bounding box.

To search, the R-tree takes a query box and, starting at the top level, sees which (if any) bounding boxes intersect it. It then expands each intersecting bounding box and sees which of the child bounding boxes inside it intersect the query box. This proceeds recursively until all intersecting boxes are searched down to the lowest level, and returns the matching objects from the lowest level.

But what if the two sets of features (say, a polygon and a set of points) that you’re intersecting have approximately the same bounding boxes? Because the polygon’s minimum bounding box is approximately the same as the set of points’ minimum bounding box, the R-tree intersects every nested bounding box and considers every point to be a possible match. Thus, using an R-tree spatial index makes the operation run no faster than it would without the spatial index!

Let’s look at how to use R-trees in Python and how to solve this limitation.

Simple example: R-tree spatial index

Python’s geopandas offers an implementation of R-tree to speed up spatial queries. Let’s say we have a polygon representing the city boundary of Walnut Creek, California:

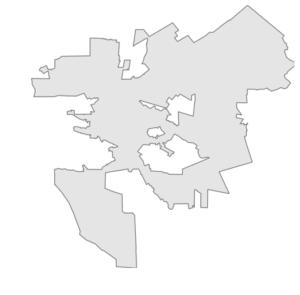
And we also have a geopandas GeoDataFrame of lat-long points representing street intersections in the vicinity of this city. Some of these points are within the city’s borders, but others are outside of them:

We can use geopandas’s R-tree spatial index to find which street intersections lie within the boundaries of the city:

spatial_index = gdf.sindex
possible_matches_index = list(spatial_index.intersection(polygon.bounds))
possible_matches = gdf.iloc[possible_matches_index]
precise_matches = possible_matches[possible_matches.intersects(polygon)]

First we have our GeoDataFrame (called gdf) create an R-tree spatial index for its geometry. Then we intersect this index with the bounding box of our polygon. This returns a set of possible matches. That is, there are no false negatives but there may be some false positives if an R-tree rectangle within the city border’s bounding box contains some points outside the city border. Finally, to identify the precise matches (those points exactly within our polygon), we intersect the possible matches with the polygon itself:

Here we can see all of the street intersections within the city of Walnut Creek in blue, and all those outside of it in red.

Advanced example: same bounding boxes

How can we use an R-tree spatial index to find the points within a polygon, if the points and the polygon have identical bounding boxes?

The R-tree index works great when the two sets of features you are intersecting or joining have different bounding boxes (such as the polygon and the points in the preceding example). However, an R-tree provides no speed up when the features’ bounding boxes are identical, because it identifies every point as a possible match because the bounding box of the polygon intersects every nested rectangle inside the index. This is a limitation of R-trees themselves.

Fortunately, we can work around this limitation in Python. Let’s say we have a polygon representing the borders of the city of Los Angeles, and a GeoDataFrame of approximately one million street intersections in and around LA:

We want to find which street intersections are within LA’s city boundary. Notice that our polygon and points have the same minimum bounding boxes, so an R-tree would offer no speed up because rectangle expansion would identify every point as a possible match.

But, we could sub-divide our polygon into smaller sub-polygons with smaller minimum bounding boxes, using shapely. I simply overlay my polygon with evenly-spaced quadrat lines, then split it into separate polygons along these lines:

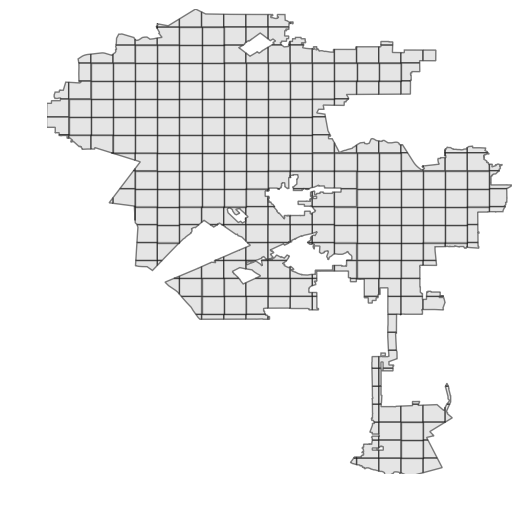
Now we can just iterate through these small sub-polygons to quickly identify which points lie within each, using the R-tree spatial index (as demonstrated in the code snippet earlier):

This spatial intersection now can take full advantage of the R-tree index and reduces the computation time from 20+ minutes down to just a few seconds. Here we can see all of the street intersections within the city of Los Angeles in blue, and all those outside of it in red:

Conclusion: R-trees and Python

Long story short, if you’re doing spatial intersections or joins with Python, you should use geopandas and its implementation of the R-tree spatial index. If you’re intersecting lots of points with a polygon – and the points and polygon have identical minimum bounding boxes – you can subdivide the polygon then intersect each sub-polygon with the points, using the index. This yields a drastic decrease in computation time.

All of my code is in this notebook in this urban data science GitHub repo.